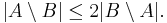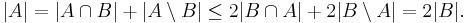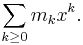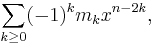Matching (graph theory)
In the mathematical discipline of graph theory, a matching or independent edge set in a graph is a set of edges without common vertices. It may also be an entire graph consisting of edges without common vertices.
| Covering-packing dualities | |
| Covering problems | Packing problems |
|---|---|
| Minimum set cover | Maximum set packing |
| Minimum vertex cover | Maximum matching |
| Minimum edge cover | Maximum independent set |
Contents |
Definition
Given a graph G = (V,E), a matching M in G is a set of pairwise non-adjacent edges; that is, no two edges share a common vertex.
A vertex is matched (or saturated) if it is incident to an edge in the matching. Otherwise the vertex is unmatched.
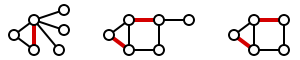
A maximal matching is a matching M of a graph G with the property that if any edge not in M is added to M, it is no longer a matching, that is, M is maximal if it is not a proper subset of any other matching in graph G. In other words, a matching M of a graph G is maximal if every edge in G has a non-empty intersection with at least one edge in M. The following figure shows examples of maximal matchings (red) in three graphs.
A maximum matching is a matching that contains the largest possible number of edges. There may be many maximum matchings. The matching number 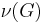 of a graph
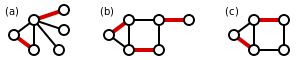
of a graph 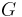 is the size of a maximum matching. Note that every maximum matching is maximal, but not every maximal matching is a maximum matching. The following figure shows examples of maximum matchings in three graphs.
is the size of a maximum matching. Note that every maximum matching is maximal, but not every maximal matching is a maximum matching. The following figure shows examples of maximum matchings in three graphs.
A perfect matching (a.k.a. 1-factor) is a matching which matches all vertices of the graph. That is, every vertex of the graph is incident to exactly one edge of the matching. Figure (b) above is an example of a perfect matching. Every perfect matching is maximum and hence maximal. In some literature, the term complete matching is used. In the above figure, only part (b) shows a perfect matching. A perfect matching is also a minimum-size edge cover. Thus, 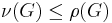 , that is, the size of a maximum matching is no larger than the size of a minimum edge cover.
, that is, the size of a maximum matching is no larger than the size of a minimum edge cover.
A near-perfect matching is one in which exactly one vertex is unmatched. This can only occur when the graph has an odd number of vertices, and such a matching must be maximum. In the above figure, part (c) shows a near-perfect matching. If, for every vertex in a graph, there is a near-perfect matching that omits only that vertex, the graph is also called factor-critical.
Given a matching M,
- an alternating path is a path in which the edges belong alternatively to the matching and not to the matching.
- an augmenting path is an alternating path that starts from and ends on free (unmatched) vertices.
One can prove that a matching is maximum if and only if it does not have any augmenting path. (This result is sometimes called Berge's lemma.)
Properties
In any graph without isolated vertices, the sum of the matching number and the edge covering number equals the number of vertices.[1] If there is a perfect matching, then both the matching number and the edge cover number are |V|/2.
If A and B are two maximal matchings, then |A| ≤ 2|B| and |B| ≤ 2|A|. To see this, observe that each edge in A \ B can be adjacent to at most two edges in B \ A because B is a matching. Since each edge in B \ A is adjacent to an edge in A \ B by maximality, we see that
Further we get that
In particular, this shows that any maximal matching is a 2-approximation of a maximum matching and also a 2-approximation of a minimum maximal matching. This inequality is tight: for example, if G is a path with 3 edges and 4 nodes, the size of a minimum maximal matching is 1 and the size of a maximum matching is 2.
Matching polynomials
A generating function of the number of k-edge matchings in a graph is called a matching polynomial. Let G be a graph and mk be the number of k-edge matchings. One matching polynomial of G is
Another definition gives the matching polynomial as
where n is the number of vertices in the graph. Each type has its uses; for more information see the article on matching polynomials.
Algorithms and computational complexity
Maximum matchings in bipartite graphs
Matching problems are often concerned with bipartite graphs. Finding a maximum bipartite matching [2] (often called a maximum cardinality bipartite matching) in a bipartite graph 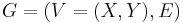 is perhaps the simplest problem. The augmenting path algorithm finds it by finding an augmenting path from each
is perhaps the simplest problem. The augmenting path algorithm finds it by finding an augmenting path from each 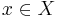 to
to  and adding it to the matching if it exists. As each path can be found in
and adding it to the matching if it exists. As each path can be found in 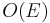 time, the running time is
time, the running time is 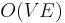 . This solution is equivalent to adding a super source
. This solution is equivalent to adding a super source  with edges to all vertices in
with edges to all vertices in  , and a super sink
, and a super sink 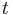 with edges from all vertices in
with edges from all vertices in  , and finding a maximal flow from
, and finding a maximal flow from  to
to 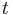 . All edges with flow from
. All edges with flow from  to
to  then constitute a maximum matching. An improvement over this is the Hopcroft-Karp algorithm, which runs in
then constitute a maximum matching. An improvement over this is the Hopcroft-Karp algorithm, which runs in 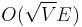 time. Another approach is based on the fast matrix multiplication algorithm and gives
time. Another approach is based on the fast matrix multiplication algorithm and gives 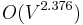 complexity,[3] which is better in theory for sufficiently dense graphs, but in practice the algorithm is slower.
complexity,[3] which is better in theory for sufficiently dense graphs, but in practice the algorithm is slower.
In a weighted bipartite graph, each edge has an associated value. A maximum weighted bipartite matching[2] is defined as a perfect matching where the sum of the values of the edges in the matching have a maximal value. If the graph is not complete bipartite, missing edges are inserted with value zero. Finding such a matching is known as the assignment problem. It can be solved by using a modified shortest path search in the augmenting path algorithm. If the Bellman-Ford algorithm is used, the running time becomes 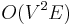 , or the edge cost can be shifted with a potential to achieve
, or the edge cost can be shifted with a potential to achieve 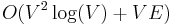 running time with the Dijkstra algorithm and Fibonacci heap. The remarkable Hungarian algorithm solves the assignment problem and it was one of the beginnings of combinatorial optimization algorithms. The original approach of this algorithm need
running time with the Dijkstra algorithm and Fibonacci heap. The remarkable Hungarian algorithm solves the assignment problem and it was one of the beginnings of combinatorial optimization algorithms. The original approach of this algorithm need 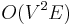 running time, but it could be improved to
running time, but it could be improved to 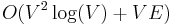 time with extensive use of priority queues.
time with extensive use of priority queues.
Maximum matchings
There is a polynomial time algorithm to find a maximum matching or a maximum weight matching in a graph that is not bipartite; it is due to Jack Edmonds, is called the paths, trees, and flowers method or simply Edmonds's algorithm, and uses bidirected edges. A generalization of the same technique can also be used to find maximum independent sets in claw-free graphs. Edmonds' algorithm has subsequently been improved to run in time 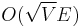 time, matching the time for bipartite maximum matching.[4] Another algorithm by Mucha and Sankowski[3], based on the fast matrix multiplication algorithm, gives
time, matching the time for bipartite maximum matching.[4] Another algorithm by Mucha and Sankowski[3], based on the fast matrix multiplication algorithm, gives 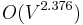 complexity.
complexity.
Maximal matchings
A maximal matching can be found with a simple greedy algorithm. A maximum matching is also a maximal matching, and hence it is possible to find a largest maximal matching in polynomial time. However, no polynomial-time algorithm is known for finding a minimum maximal matching, that is, a maximal matching that contains the smallest possible number of edges.
Note that a maximal matching with k edges is an edge dominating set with k edges. Conversely, if we are given a minimum edge dominating set with k edges, we can construct a maximal matching with k edges in polynomial time. Therefore the problem of finding a minimum maximal matching is essentially equal to the problem of finding a minimum edge dominating set.[5] Both of these two optimisation problems are known to be NP-hard; the decision versions of these problems are classical examples of NP-complete problems.[6] Both problems can be approximated within factor 2 in polynomial time: simply find an arbitrary maximal matching M.[7]
Counting problems
The problem of determining the number of perfect matchings in a given graph is #P Complete (see Permanent). However, a remarkable theorem of Kasteleyn states that the number of perfect matchings in a planar graph can be computed exactly in polynomial time. Also, for bipartite graphs, the problem can be approximately solved in polynomial time.[8] That is, for any ε>0, there is a probabilistic polynomial time algorithm that determines, with high probability, the number of perfect matchings M within an error of at most εM.
For the problem of determining the total number of matchings in a given graph, see Hosoya index.
Notes
König's theorem states that, in bipartite graphs, the maximum matching is equal in size to the minimum vertex cover. Via this result, the minimum vertex cover, maximum independent set, and maximum vertex biclique problems may be solved in polynomial time for bipartite graphs.
The marriage theorem provides a characterization of bipartite graphs which have a perfect matching and the Tutte theorem provides a characterization for arbitrary graphs.
A perfect matching is a spanning 1-regular subgraph, a.k.a. a 1-factor. In general, a spanning k-regular subgraph is a k-factor.
Applications
A Kekulé structure of an aromatic compound consists of a perfect matching of its carbon skeleton, showing the locations of double bonds in the chemical structure. These structures are named after Friedrich August Kekulé von Stradonitz, who showed that benzene (in graph theoretical terms, a 6-vertex cycle) can be given such a structure.[9]
The Hosoya index is the number of non-empty matchings plus one; it is used in computational chemistry and mathematical chemistry investigations for organic compounds.
See also
- Vertex independent set
- Dulmage–Mendelsohn decomposition
- Stable matching
- Skew-symmetric graph
References
- ↑ Gallai, Tibor (1959), "Über extreme Punkt- und Kantenmengen", Ann. Univ. Sci. Budapest, Eotvos Sect. Math. 2: 133–138.
- ↑ 2.0 2.1 West, Douglas Brent (1999), Introduction to Graph Theory (2nd ed.), Prentice Hall, Chapter 3, ISBN 0-13-014400-2
- ↑ 3.0 3.1 Mucha, M.; Sankowski, P. (2004), "Maximum Matchings via Gaussian Elimination", Proc. 45st IEEE Symp. Foundations of Computer Science, pp. 248–255, http://www.mimuw.edu.pl/~mucha/pub/mucha_sankowski_focs04.pdf
- ↑ Micali, S.; Vazirani, V. V. (1980), "An
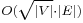 algorithm for finding maximum matching in general graphs", Proc. 21st IEEE Symp. Foundations of Computer Science, pp. 17–27, doi:10.1109/SFCS.1980.12.
algorithm for finding maximum matching in general graphs", Proc. 21st IEEE Symp. Foundations of Computer Science, pp. 17–27, doi:10.1109/SFCS.1980.12. - ↑ Yannakakis, Mihalis; Gavril, Fanica (1980), "Edge dominating sets in graphs", SIAM J. Appl. Math. 38 (3): 364–372, doi:10.1137/0138030.
- ↑ Garey, Michael R.; Johnson, David S. (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness, W.H. Freeman, ISBN 0-7167-1045-5. Edge dominating set (decision version) is discussed under the dominating set problem, which is the problem GT2 in Appendix A1.1. Minimum maximal matching (decision version) is the problem GT10 in Appendix A1.1.
- ↑ Ausiello, Giorgio; Crescenzi, Pierluigi; Gambosi, Giorgio; Kann, Viggo; Marchetti-Spaccamela, Alberto; Protasi, Marco (2003), Complexity and Approximation: Combinatorial Optimization Problems and Their Approximability Properties, Springer. Minimum edge dominating set (optimisation version) is the problem GT3 in Appendix B (page 370). Minimum maximal matching (optimisation version) is the problem GT10 in Appendix B (page 374). See also Minimum Edge Dominating Set and Minimum Maximal Matching in the web compendium.
- ↑ Wai Jing Law (2009). "Approximately Counting Perfect And General Matchings in Bipartite and General Graphs". Ph.D. dissertation (Duke University). http://dukespace.lib.duke.edu/dspace/bitstream/10161/1054/1/D_Law_Wai_a_200904.pdf.
- ↑ See, e.g., Trinajstić, Nenad; Klein, Douglas J.; Randić, Milan (1986), "On some solved and unsolved problems of chemical graph theory", International Journal of Quantum Chemistry 30 (S20): 699–742, doi:10.1002/qua.560300762.
Further reading
- Lovász, László; M.D. Plummer (1986). Matching Theory. North-Holland. ISBN 0444879161.
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest and Clifford Stein (2001). Introduction to Algorithms (second ed.). MIT Press and McGraw-Hill. Chapter 26, pp. 643–700. ISBN 0-262-53196-8.
- András Frank (2004). On Kuhn's Hungarian Method - A tribute from Hungary. Technical Report Egerváry Research Group.
- Michael L. Fredman and Robert E. Tarjan (1987). "Fibonacci heaps and their uses in improved network optimization algorithms". Journal of the ACM (ACM Press) 34 (3): 595–615. doi:10.1145/28869.28874.
- S. J. Cyvin and Ivan Gutman (1988). Kekule Structures in Benzenoid Hydrocarbons. Springer-Verlag.